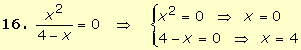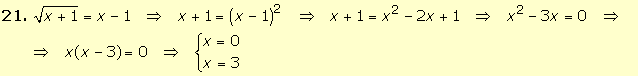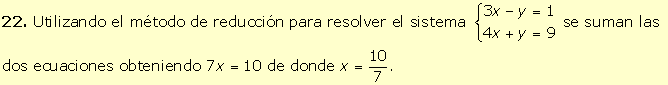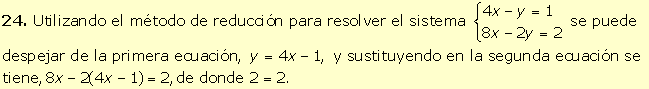|
1.
3x + 1 = 2
Þ
3x = 3
|
·
Desarrollo
correcto
· Teoría |
|
2.
4x = 5
Þ
x = 5 - 4 = 1 |
· Desarrollo
correcto
· Teoría |
|
3.
6x = 0
Þ
x = 0 - 6 = -6 |
· Desarrollo
correcto
· Teoría |
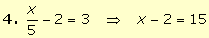 |
· Desarrollo
correcto
· Teoría |
|
5.
4x + 1 = -12
Þ
x + 1 = -3
Þ
x = -4 |
· Desarrollo
correcto
· Teoría |
|
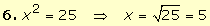
|
· Desarrollo
correcto
· Teoría |
|
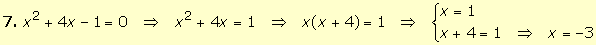 |
· Desarrollo
correcto
· Teoría |
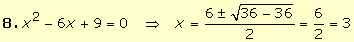
Por
tanto, x = 3 es raíz simple del polinomio x2 -
6x + 9. |
· Desarrollo
correcto
· Teoría |
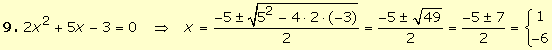 |
· Desarrollo
correcto
· Teoría |
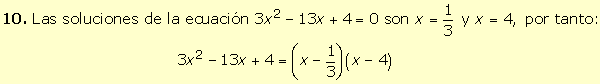 |
· Desarrollo
correcto
· Teoría |
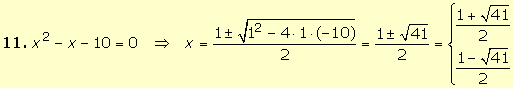
Por
tanto, la ecuación no tiene soluciones reales. |
· Desarrollo
correcto
· Teoría |
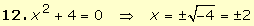 |
· Desarrollo
correcto
· Teoría |
|
13.
Al resolver la ecuación x3 -
2x2 -
5x + 6 = 0 dividiendo por Ruffini:
1
-2 -5 6
1 1
-1 -6
1
-1 -6 |0
-2 -2 6
1 -3 |0
3
3
1 |0
se
obtiene que las soluciones de la ecuación son x = -1, x = 2 y
x = -3.
|
· Desarrollo
correcto
· Teoría |
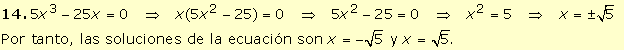 |
· Desarrollo
correcto
· Teoría |
|
15.
Al resolver la ecuación bicuadrada x4 -
8x2 +
16 = 0 con el cambio t = x2
se obtiene la ecuación de segundo grado t2 –
8t + 16 = 0 cuyas soluciones son:
 |
· Desarrollo
correcto
· Teoría |
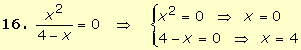
Por
tanto, las soluciones de la ecuación son x = 0 y x = 4. |
· Desarrollo
correcto
· Teoría |
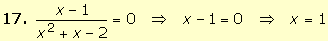
Por
tanto, la solución de la ecuación es x = 1. |
· Desarrollo
correcto
· Teoría |
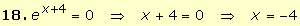 |
· Desarrollo
correcto
· Teoría |
|
19.
Despejando el exponente de la ecuación e3x+4 =
2 queda 3x + 4 = 2. |
· Desarrollo
correcto
· Teoría |
|
20.
ln(x-5) = 0
Þ
x - 5 = 0 |
· Desarrollo
correcto
· Teoría |
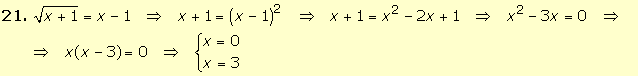
Por
tanto, las soluciones de la ecuación son x = 0 y x = 3. |
· Desarrollo
correcto
· Teoría |
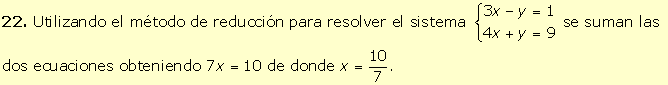 |
· Desarrollo
correcto
· Teoría |

Por
tanto, el sistema tiene dos soluciones: “x = -2, y = 0” y “x
= 1 , y = 0”. |
· Desarrollo
correcto
· Teoría |
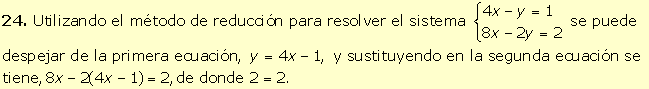
Por
tanto, la solución del sistema es x = 0, y = -1. |
· Desarrollo
correcto
· Teoría |

Por
tanto, la solución del sistema inicial es x = 8, y = -2. |
· Desarrollo
correcto
· Teoría |