ACTIVIDAD DE APRENDIZAJE A TRAVÉS DEL DESCUBRIMIENTO DE ERRORES EN LA ASIGNATURA "MATEMÁTICAS I" DE LOS GRADOS DE CARÁCTER ECONÓMICO

Autoras: Gloria Jarne, Esperanza Minguillón, Trinidad Zabal

 

Cuestionario 6: Funciones reales de una variable real I

Encuentra el error cometido en cada uno de los siguientes desarrollos matemáticos y piensa cómo sería el desarrollo correcto y la teoría (definición, propiedad, ...) utilizada en la corrección del error.

1.  El dominio de la función f(x) = ln(x2 - 9) es el conjunto D = {xÎRç ln(x2 - 9) >0}

· Desarrollo correcto

· Teoría

· Desarrollo correcto

· Teoría

· Desarrollo correcto

· Teoría

· Desarrollo correcto

· Teoría

· Desarrollo correcto

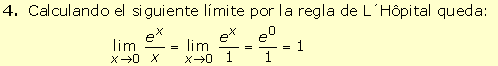· Teoría

6. La función f(x) = x2 – x es continua en [-1, 3] y verifica  f(-1) = 2, f(3) = 6. Al tener el mismo signo f(-1) y f(3) se puede asegurar, aplicando el teorema de Bolzano, que esta función no se anula en ningún punto del intervalo [-1, 3].

· Desarrollo correcto

· Teoría

7.  La función f(x) = 3/x  verifica que f(-1) = -3 y f (1) = 3 tienen distinto signo. Aplicando el teorema de Bolzano se puede asegurar que esta función se anula en algún punto del intervalo [-1, 1].

· Desarrollo correcto

· Teoría

8. La función f(x)= x2 -2x +3 en el intervalo [0, 4] no tiene máximo global.

· Desarrollo correcto

· Teoría
9. La función  f(x) = x2 -2x + 6 es continua en el intervalo [0, 3] y verifica que  f(0) = 6 < f(3) = 9. Aplicando el Teorema de Weierstrass se puede asegurar que f alcanza su valor mínimo en x = 0 y su valor máximo en x = 3.

· Desarrollo correcto

· Teoría

· Desarrollo correcto

· Teoría

· Desarrollo correcto

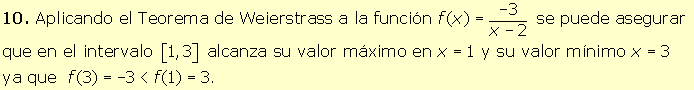· Teoría
12. Si una función f(x) es continua y tiene mínimos relativos en un intervalo [a, b], entonces tiene un mínimo global en [a, b] que se alcanza en el mínimo relativo donde la función tome el menor valor.

· Desarrollo correcto

· Teoría

 

 

Volver a página inicial