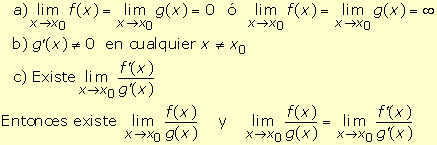|
1.
El dominio de la función f(x) = lng(x) es D = {xÎRç
g(x) >0} |
|
2.
Para resolver las indeterminaciones del tipo 1+∞
se puede utilizar la fórmula:
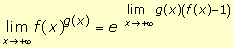 |
|
3.
Para resolver las indeterminaciones del tipo 1+∞
se puede utilizar la fórmula:
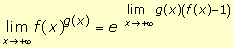 |
|
4.
Regla de l’ Hôpital
Si f y g son funciones continuas y derivables en un intervalo
abierto que contiene a un punto x0 verificando:
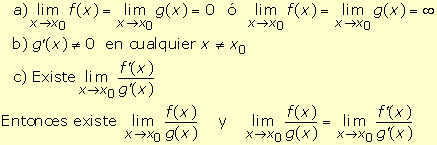 |
|
5.
Regla de l’ Hôpital
Si f y g son funciones continuas y derivables en un intervalo
abierto que contiene a un punto x0 verificando:
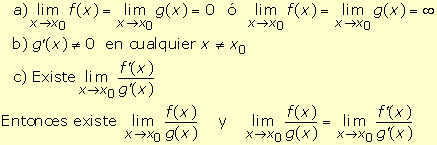 |
|
6.
Teorema de Bolzano: Si una función f(x) es continua en [a,
b] y verifica que el signo de f(a) es distinto del signo de
f(b) entonces existe algún punto cÎ[a,
b] en el que esta función se anula, es decir, f(c)=0. |
|
7.
Teorema de Bolzano: Si una función f(x) es continua en [a,
b] y verifica que el signo de f(a) es distinto del signo de
f(b) entonces existe algún punto cÎ[a,
b] en el que esta función se anula, es decir, f(c)=0. |
|
8.
Teorema de Weiertrass:
Si una función f(x) es continua en el intervalo cerrado y
acotado, entonces alcanza valor máximo y valor mínimo en dicho intervalo. |
|
9.
Teorema de Weiertrass:Si
una función f(x)
es continua en un intervalo cerrado y acotado, entonces alcanza valor máximo
y valor mínimo en dicho intervalo.
Además,
los únicos puntos en los que f puede alcanzar dichos valores son los
puntos del interior del intervalo en los que hay óptimos locales y los
extremos del intervalo. |
|
10.
Teorema de Weiertrass:Si
una función f(x) es continua en un intervalo cerrado y
acotado, entonces alcanza valor máximo y valor mínimo en dicho intervalo. |
|
11.
Teorema de Weiertrass:
Si una
función f(x) es continua en el intervalo cerrado y acotado,
entonces alcanza valor máximo y valor mínimo en dicho intervalo. |
|
12.
Teorema de Weiertrass:Si
una función f(x) es continua en el intervalo cerrado y
acotado, entonces alcanza valor máximo y valor mínimo en dicho intervalo.
Hay que
tener en cuenta que el valor mínimo (máximo) de la función en [a,
b] se alcanza en un mínimo (máximo) relativo o en alguno de los extremos
del intervalo a, b. |