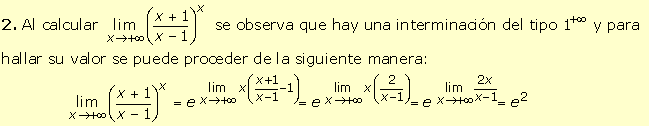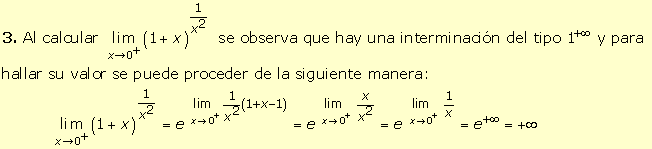1. El dominio de la función f(x) = ln(x²- 9) es el conjunto D = {xÎRç x²- 9 >0}, resolviendo la inecuación x² - 9 >0 se obtiene D = (-¥, 3) È (3, +¥).

6. La función f(x) = x² – x es continua en [-1, 3] y verifica f(-1) = 2, f(3) = 6. Al tener el mismo signo f(-1) y f(3) no se puede aplicar el teorema de Bolzano.

7. La función f(x) = 3/x no es continua en x = 0, por tanto, f(x) = 3/x no es continua en [-1, 1] y no se puede aplicar el teorema de Bolzano.

8. La función f(x)= x² -2x +3 en el intervalo [0, 4] es continua, por lo que según el teorema de Weiertrass alcanza en él un máximo y un mínimo global.

9. La función f(x) = x² - 2x +6 es continua en el intervalo [0, 3], por tanto, aplicando el Teorema de Weierstrass, se puede asegurar que f alcanza un valor máximo y un valor mínimo en dicho intervalo.

Para saber donde alcanza f dichos valores se han de considerar los extremos del intervalo y aquellos puntos del interior del intervalo en los que f tiene óptimos locales.

En primer lugar se estudia la existencia de óptimos locales en (0, 3). Al ser la función f derivable se hallan los puntos que anulen a la primera derivada:

f’(x) = 0, equivalentemente, 2x - 2 = 0, de donde x = 1

Como f”(x) = 2, se tiene que f”(1) = 2 > 0, luego f alcanza un mínimo local en x = 1.

Así, los candidatos a ser los puntos donde f alcanza el valor máximo y el valor mínimo son x = 1, x = 0 y x = 3. Calculando las imágenes de f en dichos puntos se tiene: f(1) = 5, f(0) = 6 y f(3) = 9. Al ser f(1) < f(0) < f(3), se tiene que en el intervalo [0, 3] la función alcanza su valor mínimo en x = 1 y su valor máximo en x = 3.

12. Si una función f(x) es continua en [a, b] y tiene mínimos relativos en dicho intervalo, entonces f(x) tiene en [a, b] un mínimo global que se alcanzará en un mínimo relativo o en alguno de los extremos del intervalo.