ACTIVIDAD DE APRENDIZAJE A TRAVÉS DEL DESCUBRIMIENTO DE ERRORES EN LA ASIGNATURA "MATEMÁTICAS I" DE LOS GRADOS DE CARÁCTER ECONÓMICO
Autoras: Gloria Jarne, Esperanza Minguillón, Trinidad Zabal
Cuestionario 5: Formas cuadráticas reales II (Clasificación)
Encuentra el error cometido en cada uno de los siguientes desarrollos matemáticos y piensa cómo sería el desarrollo correcto y la teoría (definición, propiedad, ...) utilizada en la corrección del error.
|
1. Q(x1, x2, x3) = x22 + 4x32 es una forma cuadrática definida positiva ya que todos los coeficientes son positivos. |
· Teoría |
|
2. La forma cuadrática Q(x1, x2, x3) = -5x12 - 3x32 es definida negativa ya que todos sus coeficientes son negativos. |
· Teoría |
|
3. Q(x1, x2, x3) = -x12 - x32 - x1x2 - x2x3 es una forma cuadrática definida negativa ya que todos los coeficientes son negativos. |
· Teoría |
 |
· Teoría |
|
5. Una forma cuadrática es semidefinida positiva o semidefinida negativa si el polinomio característico de su matriz asociada tiene algún valor propio nulo. |
· Teoría |
|
6. Si todos los menores principales de la matriz asociada a una forma cuadrática son negativos entonces la forma cuadrática es definida negativa. |
· Teoría |
|
7. Si los menores principales de una matriz A simétrica de orden 3 son ïA1ï = -2, ïA2ï = 4 y ïA3ï = -6, entonces la forma cuadrática definida por dicha matriz es indefinida ya que hay menores principales positivos y negativos. |
· Teoría |
|
8. Si los valores propios de una matriz A simétrica de orden 3 son l1 = -2, l2 = 3 y l3 = -8, entonces la forma cuadrática definida por dicha matriz es definida negativa. |
· Teoría |
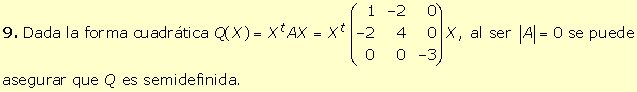 |
· Teoría |
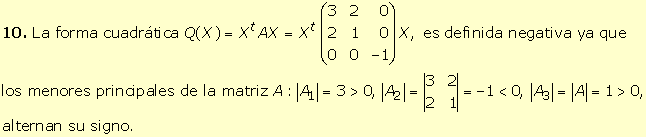 |
· Teoría |
|
11. Las formas cuadráticas Q(x1, x2, x3) = x12 - 2x22 - 5x32 y Q(y1, y2, y3) = 2y12 + y22 -5y32 son expresiones diagonales de una misma forma cuadrática ya que ambas tienen el mismo signo (son indefinidas). |
· Teoría |
| 12. Una forma cuadrática que es indefinida en R3, será indefinida en cualquier subconjunto de R3. |
· Teoría |
 |
· Teoría |
 |
· Teoría |
 |
· Teoría |
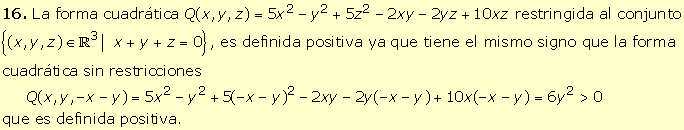 |
· Teoría |
Volver a página inicial