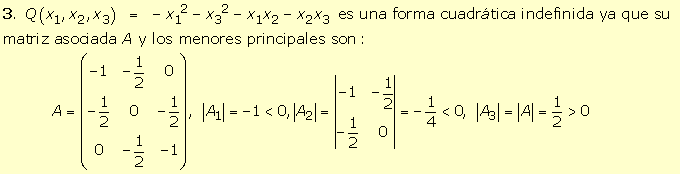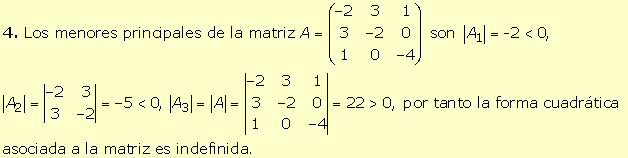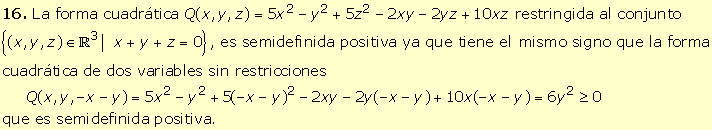|
Cuestionario 5:
Formas cuadráticas reales II (Clasificación)
Desarrollos correctos
|
1.
Q(x1,
x2, x3) = x22
+ 4x32 = 0x22 + 1x22
+ 4x32 es una forma cuadrática semidefinida
positiva ya que tiene por coeficientes 0, 1 y 4, que son positivos y cero. |
|
2.
La forma cuadrática
Q(x1,
x2, x3) = -5x12
- 3x32
= -5x12
+ 0x22 - 3x32
es semidefinida negativa ya que sus coeficientes, -5, 0 y -3, son negativos
y cero. |
|
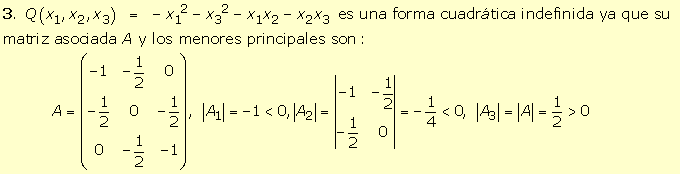 |
|
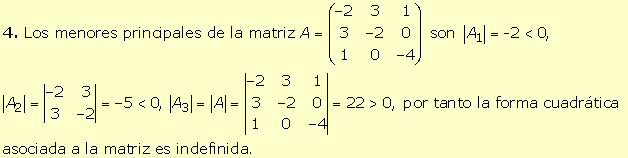 |
|
5.
Una forma cuadrática es semidefinida positiva o semidefinida negativa si el
polinomio característico de su matriz asociada tiene algún o algunos valores
propios nulos y el resto son todos son positivos o negativos
respectivamente. |
|
6.
Si todos los menores principales de la matriz asociada a una forma
cuadrática son negativos entonces la forma cuadrática es indefinida. |
|
7.
Si los menores principales de una matriz A simétrica de orden 3 son
ïA1ï
= -2, ïA2ï
= 4 y ïA3ï
= -6, entonces la forma cuadrática definida por dicha matriz es definida
negativa ya que los menores principales van alternando el signo comenzando
por negativo. |
|
8.
Si los valores propios de una matriz A simétrica de orden 3 son
l1
= -2, l2
= 3 y l3
= -8,
entonces la forma cuadrática definida por dicha matriz es indefinida. |
 |
 |
|
11.
Las formas cuadráticas
Q(x1,
x2, x3) = x12
- 2x22 - 5x32 y
Q(y1, y2, y3) =
2y12 + y22 – 5y32
no son expresiones diagonales de una misma forma
cuadrática ya que no tienen la misma signatura, es decir, el número de
coeficientes positivos y negativos no coinciden. |
|
12.
Si una forma cuadrática es indefinida en R3, entonces en un
subconjunto de R3 puede tener cualquier signo. |
 |
 |
 |
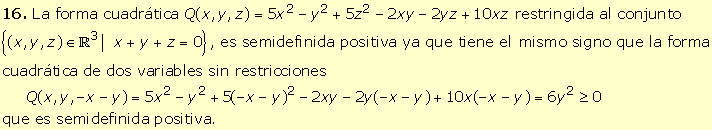 |
Volver a página inicial
|