|
1.
Dados z1
= -3+2i, z2
= 1+i, z3
= 5-i y z4
= -2-3i, calcular:
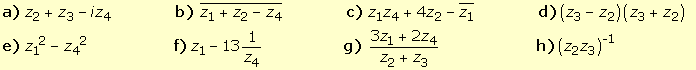 |
·
Solución
·
Ayuda
|
|
2.
Calcular:
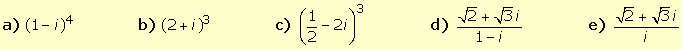 |
·
Solución
·
Ayuda
|
|
3.
Si z = 1+i, calcular el número z' que verifica
1/z' + z = 1.
|
·
Solución
·
Ayuda
|
|
4.
¿Cómo ha de ser un
número complejo para que el cociente con su conjugado sea un número real?.
|
·
Solución
·
Ayuda
|
|
5.
Calcular los números
reales k que verifican:
a)
(2+ki)/(k+i)
es un número real.
b)
(2+i)/(k+i)
tiene su parte real e imaginaria iguales.
|
·
Solución
·
Ayuda
|
|
6.
Determinar una ecuación
polinómica de coeficientes reales de grado 3 que tenga entre sus soluciones
en C los números -1/2 y 5-i. |
·
Solución
·
Ayuda
|
|
7.
Resolver en R y en C las
siguientes ecuaciones:
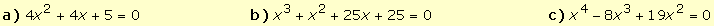
|
·
Solución
·
Ayuda
|
|
 |
·
Solución
·
Ayuda
|
|
9.
Escribir los siguientes
números complejos en forma binómica:
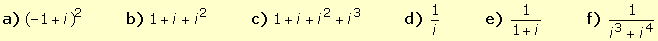 |
·
Solución
·
Ayuda
|
|
10.
Realizar las siguientes
operaciones expresando los resultados en forma binómica:
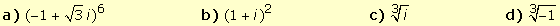 |
·
Solución
·
Ayuda
|
|
11.
Resolver en el conjunto de
los números complejos la ecuación
z4
+ 16 = 0.
|
·
Solución
·
Ayuda
|