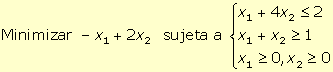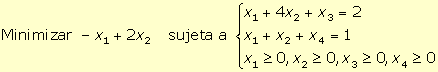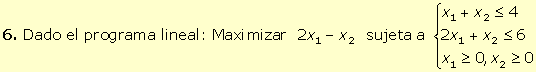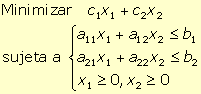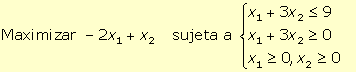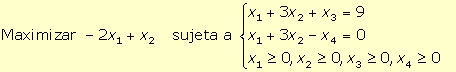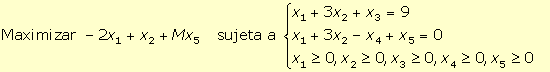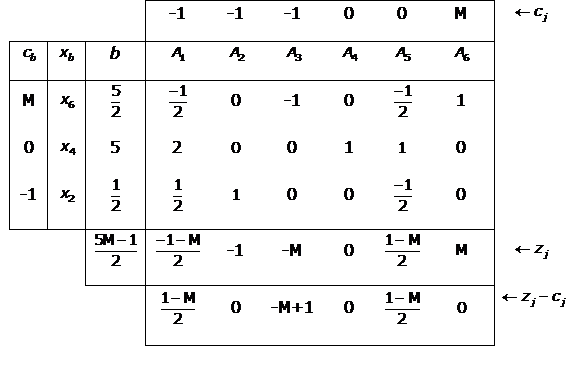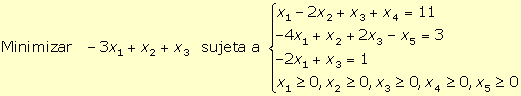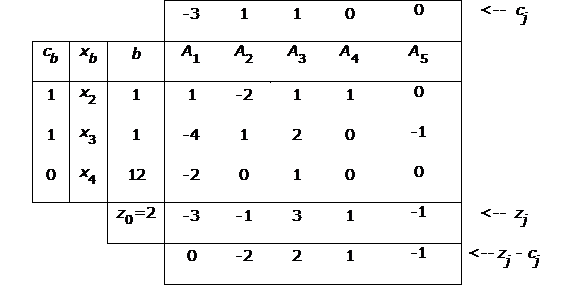Cuestionario 6

Encuentra el error cometido en cada uno de los siguientes desarrollos matemáticos y piensa cómo sería el desarrollo correcto y la teoría (definición, propiedad, ...) utilizada en la corrección del error. En este cuestionario hay que tener en cuenta que los errores no se encuentran en las operaciones realizadas.

1. Para obtener la forma estándar del programa lineal:

se han de introducir dos variables de holgura (x₃ y x₄), una en cada restricción, para

convertirlas en restricciones de igualdad, obteniéndose:

· Desarrollo correcto

· Teoría

2. Para obtener la forma estándar del programa lineal:

se han de introducir dos variables de holgura (x₃ y x₄), una en cada restricción, para

convertirlas en restricciones de igualdad, obteniéndose:

· Desarrollo correcto

· Teoría

3. Aplicando el algoritmo del simplex a un programa lineal de maximización en el que x₃ y x₄ son las variables de holgura se obtiene la siguiente tabla:

			1	-1	0	0	<-- cj
cb	xb	b	A1	A2	A3	A4
0	x3	1	0	1	1	-1
1	x1	3	1	1	0	1
		z0=3	1	1	0	1	<-- zj
			0	2	0	1	<-- zj - cj

Esta tabla corresponde a una solución óptima ya que todos los zj - cj son no negativos.

La solución asociada a esta tabla se obtiene tomando como valor de las variables básicas los coeficientes de dichas variables en la función objetivo (columna cb) y dando el valor 0 a las variables no básicas, es decir (x1, x2, x3, x4) = (1, 0, 0, 0).

Por tanto, el máximo del programa se alcanza en x1 = 1, x2 = 0 siendo este valor máximo z0 = 3.

· Desarrollo correcto

· Teoría

4. Aplicando el algoritmo del simplex a un programa lineal de maximización se obtiene la siguiente tabla inicial.

			1	1	0	0	0	<-- cj
cb	xb	b	A1	A2	A3	A4	A5
0	x3	2	-1	1	1	0	0
0	x4	6	1	2	0	1	0
0	x5	6	2	1	0	0	1
		z0=0	0	0	0	0	0	<-- zj
			-1	-1	0	0	0	<-- zj - cj

Esta tabla corresponde a una solución óptima ya que zj - cj ≤ 0 para todo j, y además es única ya que los zj - cj de las variables no básicas son negativos. Luego la única solución óptima es (0, 0, 2, 6, 6).

· Desarrollo correcto

· Teoría

se introducen las variables de holgura x3 y x4 en la primera y segunda restricción respectivamente, obteniéndose la siguiente tabla inicial para aplicar el algoritmo del simplex:

			2	-1	0	0	<-- cj
cb	xb	b	A1	A2	A3	A4
0	x3	4	1	1	1	0
0	x4	6	2	1	0	1
		z0=0	0	0	0	0	<-- zj
			-2	1	0	0	<-- zj - cj

Al ser un programa de minimización, esta tabla no corresponde a una solución óptima ya que z1 – c1 = -2 < 0. Por tanto, entra como variable básica x1 y para saber cuál deja de ser básica se considera:

mínimo {4/1, 6/2} = 3

saliendo así de la base x4.

Considerando como elemento pivote el señalado en negrita en la tabla (a21), la siguiente tabla es:

			2	-1	0	0	<-- cj
cb	xb	b	A1	A2	A3	A4
0	x3	1	0	1/2	1	-1/2
2	x1	3	1	1/2	0	1/2
		z0=6	2	1	0	1	<-- zj
			0	2	0	1	<-- zj - cj

que corresponde a una solución óptima ya que todos los zj - cj son no negativos y además la solución (3, 0, 1, 0) es única ya que los zj - cj de las variables no básicas son positivos.

· Desarrollo correcto

· Teoría

se introducen las variables de holgura x3 y x4 en la primera y segunda restricción respectivamente, obteniéndose la siguiente tabla inicial para aplicar el algoritmo del simplex:

			2	-1	0	0	<-- cj
cb	xb	b	A1	A2	A3	A4
0	x3	4	1	1	1	0
0	x4	6	2	1	0	1
		z0=0	0	0	0	0	<-- zj
			-2	1	0	0	<-- zj - cj

Esta tabla no corresponde a una solución óptima ya que z1 – c1 = -2 < 0. Por tanto, entra como variable básica x1 y para saber cuál deja de ser básica, al ser un problema de maximización, se considera:

máximo {4/1, 6/2} = 4

saliendo así de la base x3.

Considerando como elemento pivote el señalado en negrita en la tabla (a11), la siguiente tabla es:

			2	1	0	0	<-- cj
cb	xb	b	A1	A2	A3	A4
2	x1	4	1	1	1	0
0	x4	-2	0	-1	-2	1
		z0=8	2	2	2	0	<-- zj
			0	1	2	0	<-- zj - cj

que corresponde a una solución óptima ya que todos los zj - cj son no negativos y además la solución (4, 0, 0, -2) es única ya que los zj - cj de las variables no básicas son positivos.

· Desarrollo correcto

· Teoría

7. Aplicando el algoritmo del simplex a un programa lineal de maximización se obtiene la siguiente tabla inicial.

			2	1	0	0	0	<-- cj
cb	xb	b	A1	A2	A3	A4	A5
0	x3	2	-1	1	1	0	0
0	x4	6	1	2	0	1	0
0	x5	6	2	1	0	0	1
		z0=0	0	0	0	0	0	<-- zj
			-2	-1	0	0	0	<-- zj - cj

Esta tabla no corresponde a una solución óptima ya que existen zj - cj < 0. Entra en la base como variable básica x1 (ya que z1 - c1 < z2 – c2) y para saber cuál deja de ser básica se considera:

mínimo {6/1, 6/2} = 3

saliendo así de la base x5.

Realizando las operaciones elementales F1 ® F1 + F2, F2 ® 2F2 – F3, F3 ® F3/2, se obtiene la siguiente tabla:

			2	1	0	0	0	<-- cj
cb	xb	b	A1	A2	A3	A4	A5
0	x3	8	0	3	1	1	0
0	x4	6	0	3	0	2	-1
2	x1	3	1	1/2	0	0	1/2
		z0=6	2	1	0	0	1	<-- zj
			0	0	0	0	1	<-- zj - cj

que corresponde a una solución óptima ya que zj - cj ≥ 0 para todo j.

· Desarrollo correcto

· Teoría

8. Aplicando el algoritmo del simplex a un programa lineal de maximización se obtiene la siguiente tabla (siendo x3 y x4 las variables de holgura):

			1	-4	0	0	<-- cj
cb	xb	b	A1	A2	A3	A4
0	x3	9	0	1	1	1
1	x1	8	1	-4	0	1
		z0=8	1	-4	0	1	<-- zj
			0	0	0	1	<-- zj - cj

Esta tabla corresponde a la solución óptima (8, 0, 9, 0) que es única al ser todos los zj - cj no negativos.

· Desarrollo correcto

· Teoría

9. Aplicando el algoritmo del simplex a un programa lineal de maximización se obtiene la siguiente tabla (siendo x4, x5 y x6 las variables de holgura):

			3	1	0	0	0	0	<-- cj
cb	xb	b	A1	A2	A3	A4	A5	A6
0	x3	3	0	1	1	1	-1	0
3	x1	5	1	2	0	1	0	0
0	x6	0	0	-6	0	-2	-5	1
		z0=15	3	6	0	3	0	0	<-- zj
			0	5	0	3	0	0	<-- zj-cj

Esta tabla corresponde a la solución óptima (5, 0, 3, 0, 0, 0) que es única ya que todos los zj - cj son no negativos y el valor máximo es z0 = 15.

· Desarrollo correcto

· Teoría

10. Se considera el programa lineal:

donde b1, b2 son números reales no negativos. La siguiente tabla se obtiene aplicando el algoritmo del simplex (siendo x3 y x4 las variables de holgura):

			-5	-1	0	0	<-- cj
cb	xb	b	A1	A2	A3	A4
-5	x1	2	1	-2/3	1/3	0
0	x4	12	0	-2/3	4/3	1
		z0=-10	-5	10/3	-5/3	0	<-- zj
			0	13/3	-5/3	0	<-- zj - cj

Esta tabla no corresponde a una solución óptima ya que z2 - c2 = 13/3 > 0. Por tanto, entra como variable básica x2 y para saber cuál deja de ser básica se considera:

mínimo {2/(-2/3), 12/(-2/3)} = -18

saliendo así de la base x4.

Considerando como elemento pivote el señalado en negrita en la tabla (a22) se obtiene la siguiente tabla:

			-5	-1	0	0	<-- cj
cb	xb	b	A1	A2	A3	A4
-5	x1	-10	1	0	-1	-1
-1	x2	-18	0	1	-2	-3/2
		z0=68	-5	-1	7	13/2	<-- zj
			0	0	7	13/2	<-- zj - cj

que tampoco corresponde a una solución óptima ya que existen zj - cj > 0.

· Desarrollo correcto

· Teoría

11. Para obtener la forma estándar del programa lineal:

se han de introducir dos variables de holgura (x₃ y x₄) una en cada restricción para

convertirlas en restricciones de igualdad, obteniéndose:

Para obtener una solución factible básica inicial asociada a la matriz identidad con la que comenzar a aplicar el algoritmo del simplex, se puede añadir una variable artificial x₅≥ 0 en la segunda restricción. En la función objetivo se introduce esta variable con un coeficiente M tan grande como se quiera. Así, el programa al que se aplica el algoritmo del simplex es:

· Desarrollo correcto

· Teoría

12. Aplicando el algoritmo del simplex a un programa lineal de minimización se obtiene la siguiente tabla donde x4 y x5 son variables de holgura, x6 es una variable artificial y M es una cantidad positiva tan grande como se quiera:

Esta tabla corresponde a una solución óptima ya que todos los zj - cj son menores o iguales que 0 y además es una solución única ya que los zj - cj de las variables no básicas son negativos.

La solución del programa es (x1, x2, x3, x4, x5, x6) = (0, 1/2, 0, 5, 0, 5/2). Por tanto, la solución del programa inicial es x1= 0, x2= 1/2, x3 = 0.

· Desarrollo correcto

· Teoría

13. Dado el programa lineal en forma estándar (x4 y x5 variables de holgura):

Se puede evitar introducir variables artificiales para obtener una solución factible básica inicial, considerando como solución inicial una solución factible básica que no esté asociada a la matriz identidad. Por ejemplo, considerando las columnas A2, A3 y A4 de la matriz que define las restricciones del programa estándar:

La tabla asociada a esta solución factible básica es:

· Desarrollo correcto

· Teoría