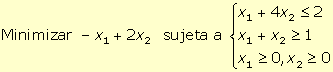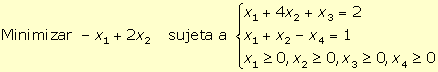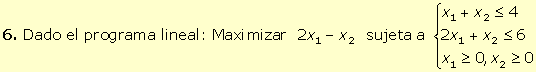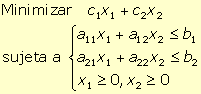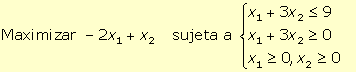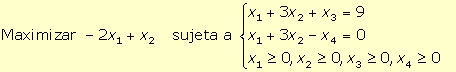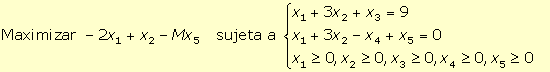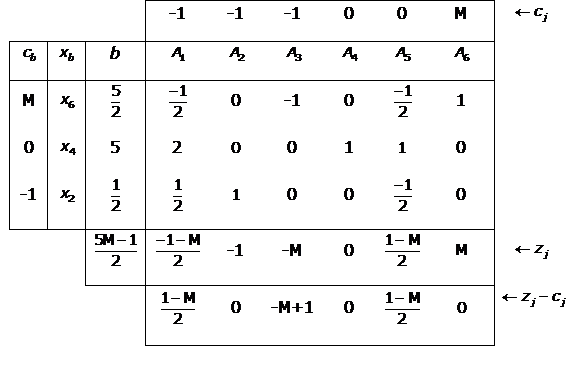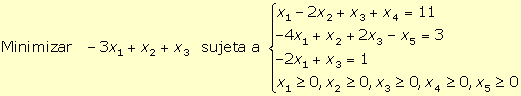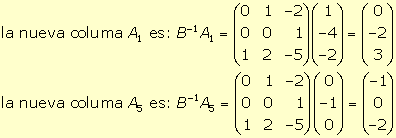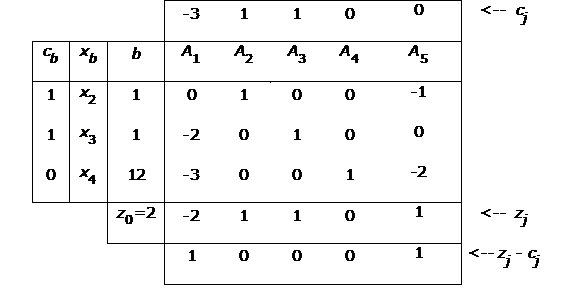|
Cuestionario 6:
Programación lineal. Algoritmo del simplex
Desarrollos correctos
|
1.
Para obtener la forma estándar del programa lineal:
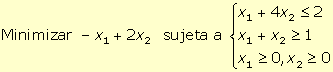
se han de introducir dos
variables de holgura (x3 y x4), una en
cada restricción, para
convertirlas en restricciones de igualdad, obteniéndose:
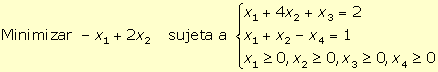 |
|
2.
Para obtener la forma estándar del programa lineal:

además de introducir una variable de holgura (x3 y x4)
en cada restricción para
convertirlas en restricciones de
igualdad, al no aparecer la restricción de no negatividad
en la variable x2 (x2 ≥ 0), se ha de
considerar el cambio x2 = u2 - v2
, con u2 ≥ 0 y v2 ≥ 0.
Así, la forma estándar del programa es:
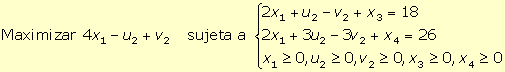 |
3.
Aplicando el algoritmo del simplex a un programa lineal de maximización en
el que x3 y
x4 son
las variables de holgura se obtiene la siguiente tabla:
|
|
|
|
1 |
-1 |
0 |
0 |
<--
cj |
|
cb |
xb |
b |
A1 |
A2 |
A3 |
A4 |
|
|
0 |
x3 |
1 |
0 |
1 |
1 |
-1 |
|
|
1 |
x1 |
3 |
1 |
1 |
0 |
1 |
|
|
|
|
z0=3 |
1 |
1 |
0 |
1 |
<--
zj |
|
|
|
|
0 |
2 |
0 |
1 |
<--
zj -
cj |
Esta tabla corresponde a una solución óptima ya que todos los zj -
cj son no negativos.
La solución asociada a esta tabla se obtiene tomando como valor de las
variables básicas los bi de
la tabla (columna b) y dando el valor 0 a las variables no básicas,
es decir (x1,
x2,
x3,
x4)
= (3, 0, 1, 0).
Por tanto, el máximo del programa se alcanza en x1 =
3, x2 =
0 siendo este valor máximo z0 =
3. |
4.
Aplicando el algoritmo del simplex a un programa lineal de maximización se
obtiene la siguiente tabla inicial.
|
|
|
|
1 |
1 |
0 |
0 |
0 |
<--
cj |
|
cb |
xb |
b |
A1 |
A2 |
A3 |
A4 |
A5 |
|
|
0 |
x3 |
2 |
-1 |
1 |
1 |
0 |
0 |
|
|
0 |
x4 |
6 |
1 |
2 |
0 |
1 |
0 |
|
|
0 |
x5 |
6 |
2 |
1 |
0 |
0 |
1 |
|
|
|
|
z0=0 |
0 |
0 |
0 |
0 |
0 |
<--
zj |
|
|
|
|
-1 |
-1 |
0 |
0 |
0 |
<--
zj -
cj |
Esta tabla no corresponde a una solución óptima ya que existen zj -
cj <
0.
|
|

se introducen las variables de holgura x3 y
x4 en
la primera y segunda restricción respectivamente, obteniéndose la siguiente
tabla inicial para aplicar el algoritmo del simplex:
|
|
|
|
2 |
-1 |
0 |
0 |
<--
cj |
|
cb |
xb |
b |
A1 |
A2 |
A3 |
A4 |
|
|
0 |
x3 |
4 |
1 |
1 |
1 |
0 |
|
|
0 |
x4 |
6 |
2 |
1 |
0 |
1 |
|
|
|
|
z0=0 |
0 |
0 |
0 |
0 |
<--
zj |
|
|
|
|
-2 |
1 |
0 |
0 |
<--
zj -
cj |
Al ser un programa de minimización, esta tabla no es óptima ya que z2 –
c2 =
1 > 0. Por tanto, entra como variable básica x2
y para saber cuál deja de ser básica se considera:
mínimo {4/1, 6/1} = 4
saliendo así de la base x3.
Considerando como elemento pivote el señalado en negrita en la tabla (a21),
la siguiente tabla es:
|
|
|
|
2 |
-1 |
0 |
0 |
<--
cj |
|
cb |
xb |
b |
A1 |
A2 |
A3 |
A4 |
|
|
-1 |
x2 |
4 |
1 |
1 |
1 |
0 |
|
|
0 |
x4 |
2 |
1 |
0 |
-1 |
1 |
|
|
|
|
z0=-4 |
-1 |
-1 |
-1 |
0 |
<--
zj |
|
|
|
|
-3 |
0 |
-1 |
0 |
<--
zj -
cj |
que corresponde a una solución óptima ya que todos los zj -
cj son
negativos o cero y además la solución (0, 4, 0, 2) es única ya que los zj -
cj de
las variables no básicas son negativos. |
|
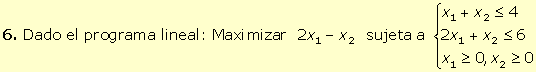
se introducen las variables de holgura x3 y
x4 en
la primera y segunda restricción respectivamente, obteniéndose la siguiente
tabla inicial para aplicar el algoritmo del simplex:
|
|
|
|
2 |
-1 |
0 |
0 |
<--
cj |
|
cb |
xb |
b |
A1 |
A2 |
A3 |
A4 |
|
|
0 |
x3 |
4 |
1 |
1 |
1 |
0 |
|
|
0 |
x4 |
6 |
2 |
1 |
0 |
1 |
|
|
|
|
z0=0 |
0 |
0 |
0 |
0 |
<--
zj |
|
|
|
|
-2 |
1 |
0 |
0 |
<--
zj -
cj |
Esta tabla no corresponde a una solución óptima ya que z1 –
c1 =
-2 < 0. Por tanto, entra como variable básica x1
y para saber cuál deja de ser básica se considera:
mínimo {4/1, 6/2} = 3
saliendo así de la base x4.
Considerando como elemento pivote el señalado en negrita en la tabla (a12),
la siguiente tabla es:
|
|
|
|
2 |
-1 |
0 |
0 |
<--
cj |
|
cb |
xb |
b |
A1 |
A2 |
A3 |
A4 |
|
|
0 |
x3 |
1 |
0 |
1/2 |
1 |
-1/2 |
|
|
2 |
x1 |
3 |
1 |
1/2 |
0 |
1/2 |
|
|
|
|
z0=6 |
2 |
1 |
0 |
1 |
<--
zj |
|
|
|
|
0 |
2 |
0 |
1 |
<--
zj -
cj |
que corresponde a una solución óptima ya que todos los zj -
cj son
no negativos y además la solución (3, 0, 1, 0) es única ya que los zj -
cj de
las variables no básicas son positivos. |
7.
Aplicando el algoritmo del simplex a un programa lineal de maximización se
obtiene la siguiente tabla inicial.
|
|
|
|
2 |
1 |
0 |
0 |
0 |
<--
cj |
|
cb |
xb |
b |
A1 |
A2 |
A3 |
A4 |
A5 |
|
|
0 |
x3 |
2 |
-1 |
1 |
1 |
0 |
0 |
|
|
0 |
x4 |
6 |
1 |
2 |
0 |
1 |
0 |
|
|
0 |
x5 |
6 |
2 |
1 |
0 |
0 |
1 |
|
|
|
|
z0=0 |
0 |
0 |
0 |
0 |
0 |
<--
zj |
|
|
|
|
-2 |
-1 |
0 |
0 |
0 |
<--
zj -
cj |
Esta tabla no corresponde a una solución óptima ya que existen zj -
cj < 0. Entra en la base como variable
básica x1
(ya que z1 -
c1
< z2 –
c2)
y para saber cuál deja de ser básica se considera:
mínimo {6/1, 6/2} = 3
saliendo así de la base x5.
Considerando como elemento pivote el señalado en negrita en la tabla (a31)
y realizando las operaciones elementales F3 ®
F3/2,
F1 ®
F1 +
F3/2,
F2 ®
F2 –
F3/2,
se obtiene la siguiente tabla:
|
|
|
|
2 |
1 |
0 |
0 |
0 |
<--
cj |
|
cb |
xb |
b |
A1 |
A2 |
A3 |
A4 |
A5 |
|
|
0 |
x3 |
5 |
0 |
3/2 |
1 |
0 |
1/2 |
|
|
0 |
x4 |
3 |
0 |
3/2 |
0 |
1 |
-1/2 |
|
|
2 |
x1 |
3 |
1 |
1/2 |
0 |
0 |
1/2 |
|
|
|
|
z0=6 |
2 |
1 |
0 |
0 |
1 |
<--
zj |
|
|
|
|
0 |
0 |
0 |
0 |
1 |
<--
zj -
cj |
que corresponde a una solución óptima ya que zj -
cj ≥
0 para todo j. |
|
8.
Aplicando el algoritmo del simplex a un programa lineal de maximización se
obtiene la siguiente tabla (siendo x3 y
x4 las
variables de holgura):
|
|
|
|
1 |
-4 |
0 |
0 |
<--
cj |
|
cb |
xb |
b |
A1 |
A2 |
A3 |
A4 |
|
|
0 |
x3 |
9 |
0 |
1 |
1 |
1 |
|
|
1 |
x1 |
8 |
1 |
-4 |
0 |
1 |
|
|
|
|
z0=8 |
1 |
-4 |
0 |
1 |
<--
zj |
|
|
|
|
0 |
0 |
0 |
1 |
<--
zj -
cj |
Esta tabla corresponde a una solución óptima ya que todos los zj -
cj son no negativos siendo la solución
(8, 0, 9, 0) y el valor máximo z0 = 8. Pero esta solución
óptima no es única ya que z2 –
c2 =
0 siendo x2 una
variable no básica.
Para encontrar otra solución óptima, entra en la base como variable básica
x2
y sale de la base x3
(ya que en la columna
A2 el único elemento
positivo es
a12).
Considerando como elemento pivote el señalado en negrita en la tabla (a12)
se obtiene la siguiente tabla:
|
|
|
|
1 |
-4 |
0 |
0 |
<--
cj |
|
cb |
xb |
b |
A1 |
A2 |
A3 |
A4 |
|
|
-4 |
x2 |
9 |
0 |
1 |
1 |
1 |
|
|
1 |
x1 |
44 |
1 |
0 |
4 |
5 |
|
|
|
|
z0=8 |
1 |
-4 |
0 |
1 |
<--
zj |
|
|
|
|
0 |
0 |
0 |
1 |
<--
zj -
cj |
que corresponde a la solución óptima (44, 9, 0, 0) y el valor máximo z0 = 8.
Por tanto, el programa lineal tiene infinitas soluciones, todos los puntos
del segmento:
l (8, 0) + (1-
l) (44, 9), con
lÎ[0, 1]
y el valor máximo de la función objetivo es 8. |
9.
Aplicando el algoritmo del simplex a un programa lineal de maximización se
obtiene la siguiente tabla (siendo x4,
x5 y
x6 las
variables de holgura):
|
|
|
|
3 |
1 |
0 |
0 |
0 |
0 |
<--
cj |
|
cb |
xb |
b |
A1 |
A2 |
A3 |
A4 |
A5 |
A6 |
|
|
0 |
x3 |
3 |
0 |
1 |
1 |
1 |
-1 |
0 |
|
|
3 |
x1 |
5 |
1 |
2 |
0 |
1 |
0 |
0 |
|
|
0 |
x6 |
0 |
0 |
-6 |
0 |
-2 |
-5 |
1 |
|
|
|
|
z0=15 |
3 |
6 |
0 |
3 |
0 |
0 |
<--
zj |
|
|
|
|
0 |
5 |
0 |
3 |
0 |
0 |
<--
zj-cj |
Esta tabla corresponde a una solución óptima ya que todos los zj -
cj son no negativos siendo la solución
(5, 0, 3, 0, 0, 0) y el valor máximo z0=15. Pero esta solución
óptima no es única ya que z5–c5=0,
siendo x5 una
variable no básica. Para encontrar otra solución óptima, entra en la base
como variable básica x5. Pero al no existir
ningún elemento positivo en la columna A5,
se deduce que existen infinitas soluciones óptimas que corresponden a los
puntos de la semirrecta:
(5, 0, 3, 0, 0, 0) + l(0,
0, 1, 0, 1, 5), con
l
≥ 0
y el valor mínimo de la función objetivo es 15. |
|
10.
Se considera el programa lineal:
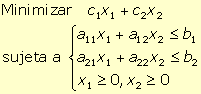
donde b1,
b2 son
números reales no negativos. La siguiente tabla se obtiene aplicando el
algoritmo del simplex (siendo x3 y
x4 las
variables de holgura):
|
|
|
|
-5 |
-1 |
0 |
0 |
<--
cj |
|
cb |
xb |
b |
A1 |
A2 |
A3 |
A4 |
|
|
-5 |
x1 |
2 |
1 |
-2/3 |
1/3 |
0 |
|
|
0 |
x4 |
12 |
0 |
-2/3 |
4/3 |
1 |
|
|
|
|
z0=-10 |
-5 |
10/3 |
-5/3 |
0 |
<--
zj |
|
|
|
|
0 |
13/3 |
-5/3 |
0 |
<--
zj -
cj |
Esta tabla no corresponde a una solución óptima ya que z2 -
c2 =
13/3 > 0. Pero como la columna A2
no tiene ningún elemento positivo, se deduce que la función objetivo no
está acotada inferiormente en el conjunto factible y, por tanto, el
programa no tiene solución óptima finita.
|
|
11.
Para obtener la forma estándar del programa lineal:
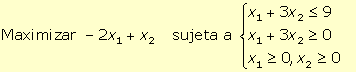
se han de introducir dos variables de holgura (x3 y x4)
una en cada restricción para
convertirlas en restricciones de igualdad, obteniéndose:
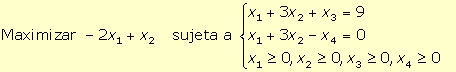
Para obtener una solución factible básica inicial asociada a la matriz
identidad con la que comenzar a aplicar el algoritmo del simplex, se puede
añadir una variable artificial x5 ≥ 0 en la segunda
restricción. Al ser un programa de maximización, en la función objetivo se
introduce esta variable con un coeficiente –M, con M tan
grande como se quiera. Así, el programa al que se aplica el algoritmo del
simplex es:
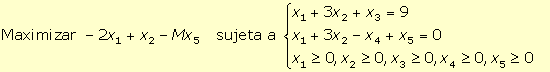 |
|
12.
Aplicando el algoritmo del simplex a un programa lineal de minimización se
obtiene la siguiente tabla donde x4 y
x5 son
variables de holgura, x6 es
una variable artificial y M es una cantidad positiva tan grande como
se quiera:
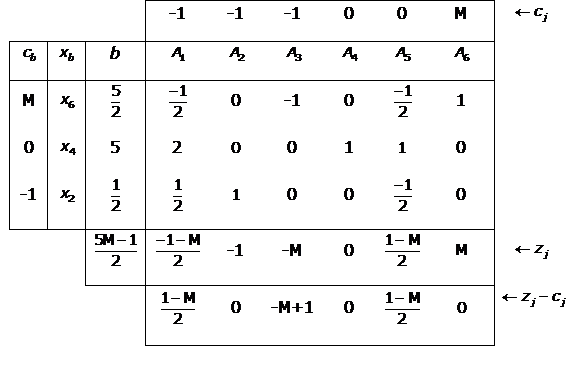
Esta tabla corresponde a una solución óptima del programa artificial ya que
todos los zj -
cj son
menores o iguales que 0. Pero como la variable artificial es una variable
básica, se concluye que el programa original no tiene solución ya que el
conjunto factible es vacío. |
|
13.
Dado el programa lineal en forma estándar (x4 y
x5 variables
de holgura):
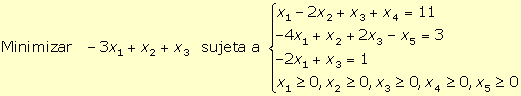
Se puede evitar introducir variables artificiales para obtener una solución
factible básica inicial, considerando como solución inicial una solución
factible básica que no esté asociada a la matriz identidad. Por ejemplo,
considerando las columnas A2,
A3 y
A4 de
la matriz que define las restricciones del programa estándar:

Para obtener la tabla asociada a esta solución factible básica es necesario
actualizar el resto de columnas de la matriz A a partir de la matriz
básica considerada. Así:
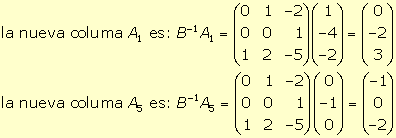
y la tabla es:
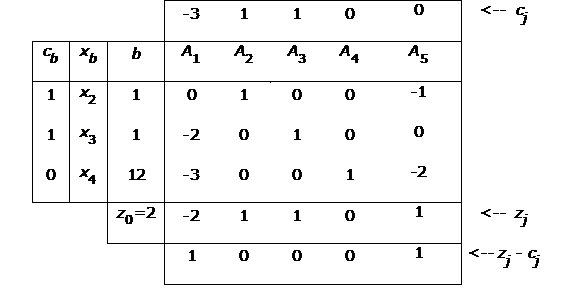 |
Volver a página inicial
|