|
1.
Una potencia es
igual al producto de la base tantas veces como indica el exponente.
|
|
2.
Para
multiplicar potencias de la misma base se suman los exponentes, es decir,
an
·
am
=
am+n. |
|
3.
Para dividir
potencias de la misma base se restan los exponentes, es decir,
an
:
am
=
am-n. |
 |
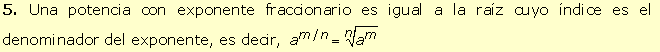 |
|
 |
|
 |
|
 |
|
9. Por definición: ln a = b si eb
= a. |
|
10. Por definición: ln a = b si
eb = a. |
|
11. Por definición: ln a = b si
eb = a. |
|
12. El
logaritmo de un producto es igual a la suma de los logaritmos de los
factores, es decir, ln(a·b)= lna + lnb siendo
a y b números positivos. |
|
13.
El logaritmo de una
fracción es igual a la diferencia de los logaritmos del numerador y del
denominador, es decir, ln(a/b) = lna – lnb siendo a, b >
0. |
|
14. El logaritmo neperiano de una potencia
es igual al exponente
por el logaritmo de la base, es decir, ln
ab
= b·
lna |
|
15. El
logaritmo de una suma no es la suma de los logaritmos: ln(a+b)
¹
lna+lnb. |