|
1.
Para cambiar de signo una fracción se cambia el signo del numerador o del
denominador.
|
|
2.
Para sumar
fracciones de distinto denominador es necesario reducirlas a común
denominador, que viene dado por el mínimo común múltiplo de los
denominadores. |
|
3.
Para sumar fracciones de distinto denominador, además de calcular el común
denominador, es necesario sustituir cada fracción por otra equivalente que
posea como denominador el mínimo común múltiplo de los denominadores. |
|
4.
Para sumar fracciones hay que poner común denominador en todos los sumandos.
Por ello es necesario sustituir cada fracción por otra equivalente que posea
como denominador el mínimo común múltiplo de los denominadores. |
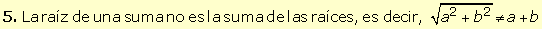 |
|
 |
|
 |
|
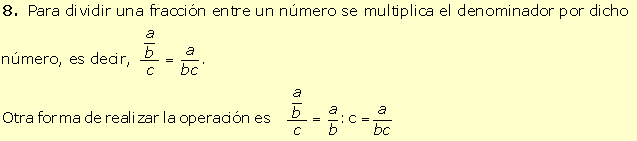 |
|
9.
Para dividir
dos fracciones se multiplica la del numerador por la inversa del
 |
|
10.
El signo
“menos” delante de un paréntesis afecta a todos los sumandos de dicho
paréntesis, es decir:
–
(a +
b) = –
a
– b |
|
11.
Propiedad
distributiva del producto respecto de la suma: a·( b+c)
= a·
b
+ a·
c |
|
12.
Propiedad
asociativa del producto, a·(b·c) = a·b·c
, por tanto, para multiplicar un número por un producto basta multiplicar
dicho número por uno de los factores. |
|
13.
El cuadrado de un binomio es igual al cuadrado del primer sumando más el
doble producto del primero por el segundo más el cuadrado del segundo, es
decir, (a+b)2
= a 2 + 2ab + b 2 |
|
14.
Suma por diferencia es igual a diferencia de cuadrados, es decir,
(a
+
b)
(a
–
b)
= a2
–
b2 |
|
15.
Aplicando la jerarquía
de las operaciones, en una expresión se realizan los productos y cocientes
antes que las sumas y las restas, salvo que exista un paréntesis que rompa
dicha jerarquía. |
|
16. Aplicando
la propiedad distributiva del producto respecto de la suma, a·b +
a·c = a·(b+c),
se tiene que para sacar factor común es necesario que dicho factor se
encuentre en todos los sumandos. |