|
1.
Hallar las
ecuaciones de las circunferencias que:
a)
tiene su centro en el punto (2, -5) y pasa por (3, 4).
b)
pasa por los puntos (-1, -3), (-4, 0) y (0, -2).
c)
uno de sus radios es el segmento que tiene por extremos los puntos (4, -1 )
y (2, 4). |
·
Solución
·
Ayuda
|
|
2.
Calcular el centro
y el radio de la circunferencia x2
+ y2
- 5x - 7y + 6 = 0. |
·
Solución
·
Ayuda
|
|
3.
Calcular el valor
del parámetro m para que la recta y = 2x sea tangente
a la circunferencia de ecuación:
x2
+ y2
- 2x + 10y + m = 0
|
·
Solución
·
Ayuda
|
|
4.
Escribir la ecuación de la circunferencia que pasa por el punto (8, 3) y es
concéntrica a la de ecuación:
x2
+
y2
- 6x
+ 2y
=
10
|
·
Solución
·
Ayuda
|
|
5. Hallar la longitud de la
cuerda común a las circunferencias:
x2
+
y2
- 4x
+ 2y
=
8 y x2
+
y2
- 12x
-10y
=
4
|
·
Solución
·
Ayuda
|
|
6.
Hallar la ecuación
reducida de la elipse que:
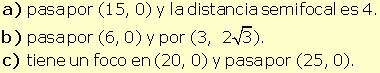
|
·
Solución
·
Ayuda
|
|
7.
Hallar los puntos de
intersección de la elipse 2x2
+ 5y2
=
7 con la recta 2x
-
y
+ 1
=
0.
|
·
Solución
·
Ayuda
|
|
8.
En la elipse
x2
+ 2y2
=
12 calcular los puntos cuya ordenada es -2.
|
·
Solución
·
Ayuda
|
|
9.
Hallar la ecuación
reducida de la hipérbola que pasa por (6,
4) y sus vértices
distan 4.
|
·
Solución
·
Ayuda
|
|
10.
Hallar los vértices y
focos de la hipérbola 9x2
- 16y2
=
144.
|
·
Solución
·
Ayuda
|
|
11.
Hallar el vértice, el
foco y la directriz de la parábola
y2
=
25x.
|
·
Solución
·
Ayuda
|
|
12.
Hallar el valor del
parámetro a para que la recta
x+y
=
a
sea tangente a la parábola de ecuación
y =
3x2
-5x+4.
|
·
Solución
·
Ayuda
|
|
13.
Hallar el eje y
vértice de la parábola
y =
2x2
+
8x
+ 1. |
·
Solución
·
Ayuda
|