|
Cuestionario 7:
Ecuaciones diferenciales de primer orden
Teoría
|
1. Dada
la solución general de una ecuación diferencial de primer orden:
F(x,y,C) = 0,
con C un número real cualquiera, la solución particular que
verifica las condiciones y(x0)= y0
es la única función F(x,y,C0) = 0 que pasa por el
punto P = (x0, y0) y se obtiene
hallando el valor de C0 que cumple F(x0,y0,C0)
= 0. |
|
2. Una
ecuación diferencial de orden uno es de variables separadas si se
puede escribir de la forma y'= f(x) g(x).
Una ecuación
diferencial es lineal de primer orden si se puede escribir de la
forma
y'+ f(x)
y = g(x). |
|
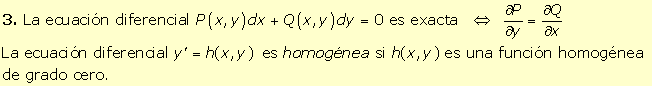 |
|
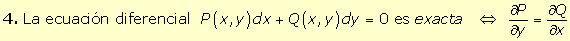 |
|
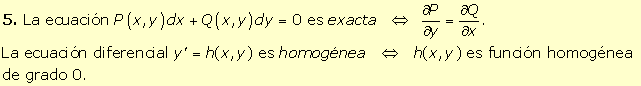 |
|
 |
|
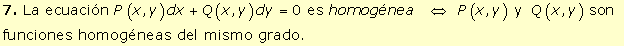 |
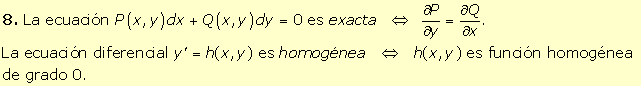 |
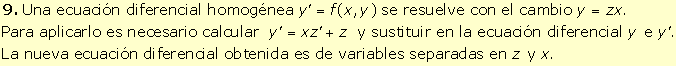 |
 |
|