El conjunto factible definido por las restricciones se representa en la siguiente figura (zona sombreada) observándose que es un conjunto cerrado y acotado.

Además al ser la función objetivo continua, el teorema de Weierstrass asegura que este programa tiene solución finita.

Por otro lado, como el programa es lineal, la solución se ha de alcanzar en los vértices del conjunto factible.

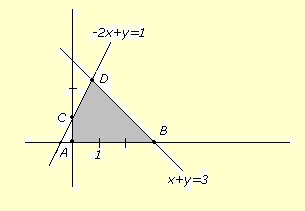
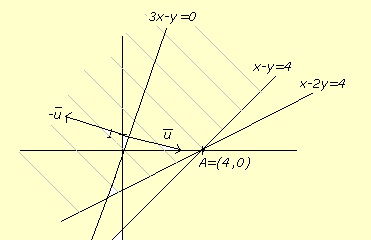
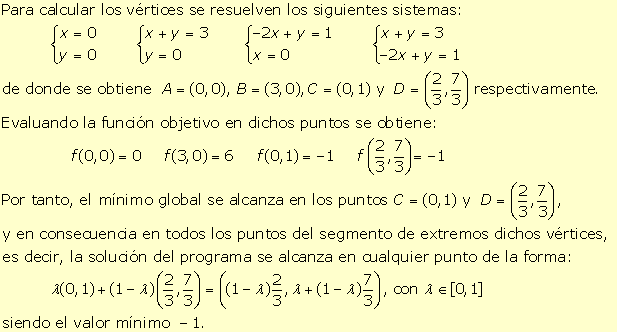Se representa el conjunto factible definido por las restricciones (zona rayada en la figura).

Al ser el programa lineal, la solución, si existe, se ha de alcanzar en los vértices del conjunto factible. En este caso no se puede asegurar la existencia de solución ya que el conjunto factible no es acotado como se observa en la figura (por lo que no se puede aplicar el Teorema de Weierstrass).

A continuación se utiliza el método gráfico para resolver el programa lineal.

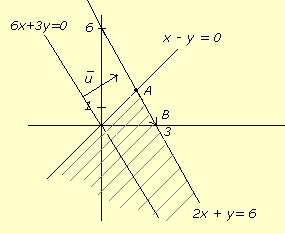
Así, la solución del programa se alcanza en cualquier punto de la semirrecta:

(2, 2) + l(1, -2) = (2+l, 2-2l), con l ≥ 0

Se representa el conjunto factible definido por las restricciones (zona rayada en la figura).