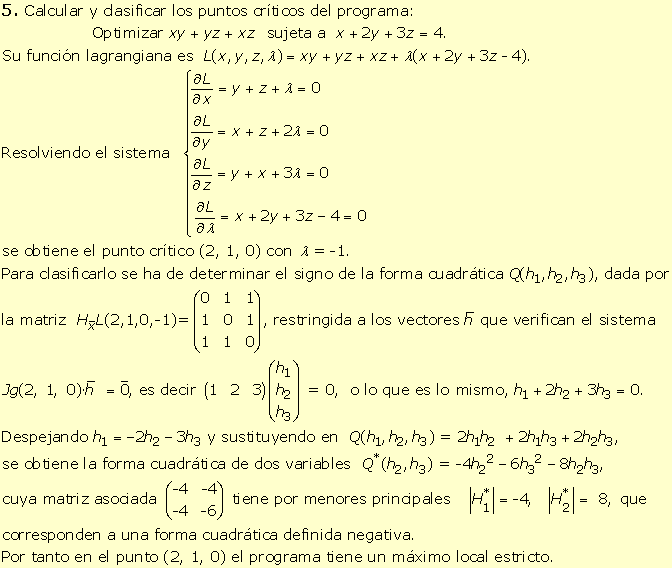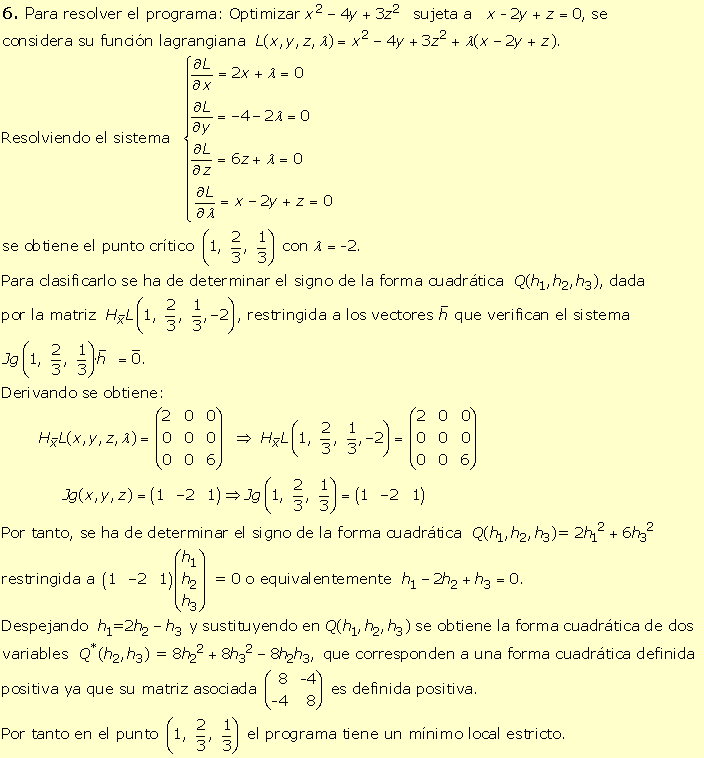|
Cuestionario 4:
Programación con restricciones de igualdad
Desarrollos correctos
|
1.
Para resolver el programa: Optimizar f(x, y) = x2
+ y2
sujeta a y - x2
= 0, por el método de eliminación de variables o de
sustitución, se despeja de la restricción del programa y= x2,
y se sustituye en la función objetivo quedando la función de una variable
g(x) = x2
+ x4.
Calculando
los óptimos de g(x) se tiene:
g'(x) = 2x + 4x3
= 0, de donde x = 0
g''(x) = 2 + 12x2
> 0, para cualquier valor de x, por tanto g es una función
estrictamente convexa.
En consecuencia, g alcanza en x= 0 un
mínimo global único.
Para
determinar el óptimo del programa, se sustituye x= 0 en y=
x2,
quedando y= 0.
Por
tanto, el programa inicial tiene un mínimo global único en el punto (0, 0). |
 |
|
3.
Calcular los puntos críticos del programa:
Optimizar f (x, y) = x2 + y
sujeta a y - 2x = 3
La función
lagrangiana es L(x, y,
l)
= x2
+
y+l
(
y
-
2x
- 3) y su gradiente viene dado por
ÑL(x,
y,
l) = (2x - 2l,
1+
l, y – 2x - 3), por ello, los puntos críticos
son las soluciones del

Luego,
el único punto crítico es (-1, 1) y su multiplicador asociado es
l
= -1. |
 |
|
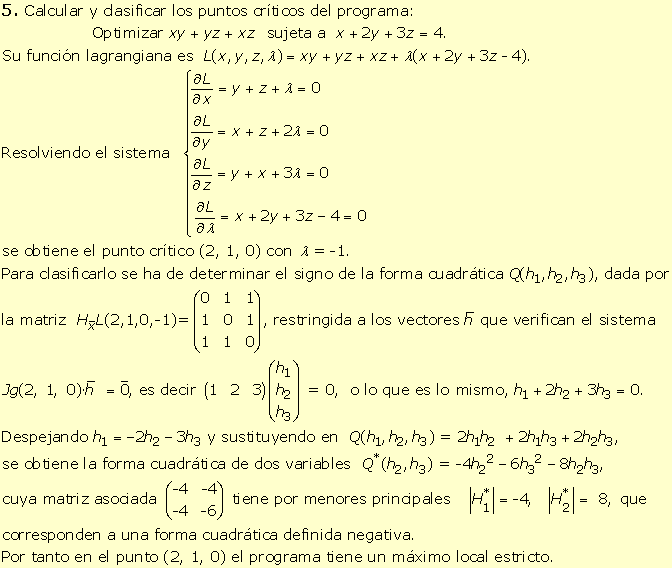 |
|
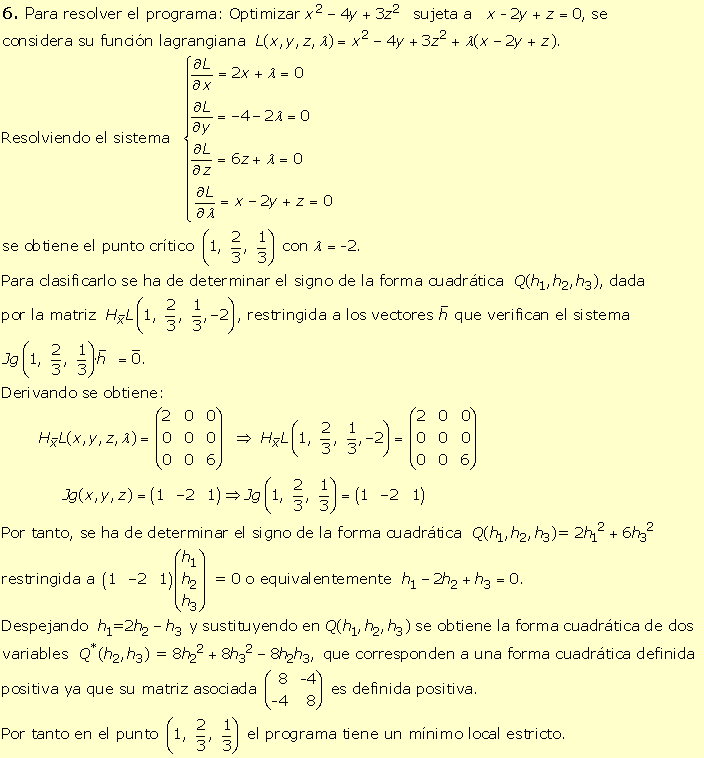 |
 |
|
 |
|
9.
Un consumidor tiene una restricción presupuestaria 8x + 3y = 480 y su
función de utilidad U(x, y), alcanza en el punto (30,
80) con
l
= -10 su máximo valor U= 2400.
Si
aumentamos en 20 euros la renta disponible entonces su utilidad máxima tiene
un incremento,
DU
@
-l
DR
= -(-10)
20
= 200.
Luego, la
nueva máxima utilidad aproximadamente es
U
@
U(30, 80)
+
200 = 2400
+
200 = 2600. |
Volver a página inicial
|