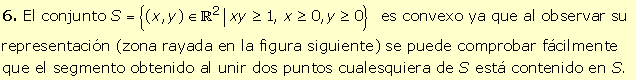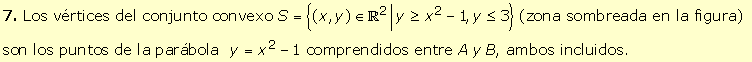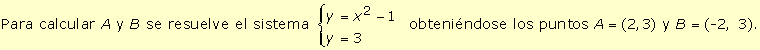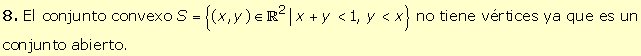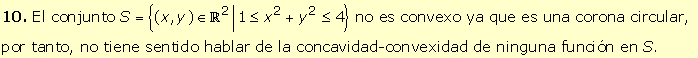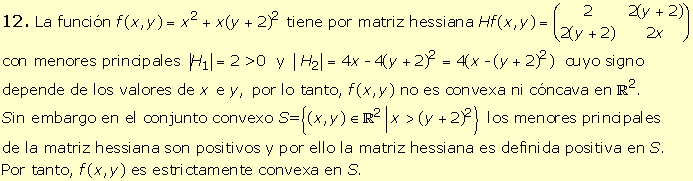|
Cuestionario 1:
Introducción a la convexidad
Desarrollos correctos
|
1.
El conjunto S
no es convexo ya que si consideramos el par de puntos C y D el
segmento que los une no está contenido en S.
 |
|
2.
El conjunto S = {(x,y)
Î
R2ç
x > y} es convexo ya que es un semiplano, y por tanto, verifica que
el segmento obtenido al unir dos puntos cualesquiera de S está
contenido en S. |

 |
|
4. El
conjunto S = {(x, y)
Î
R2
ç
x2 + y2 = 1} es una circunferencia por
tanto no es un conjunto convexo ya que tomando dos puntos distintos de dicha
circunferencia, el segmento que los une no está contenido en ella. |
|
5.
El conjunto S = {(x, y) Î
R2
ç
1≤ x2 + y2 ≤ 4} no es un conjunto convexo
ya que al observar su representación (zona sombreada en la figura siguiente)
se puede comprobar que existe algún par de puntos de S de forma que
el segmento que los une no está contenido en S (por ejemplo A
y B).
 |
|
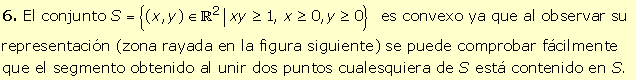
 |
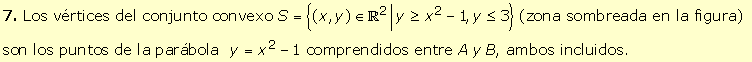
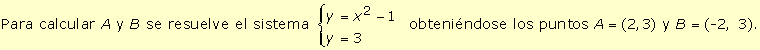 |
|
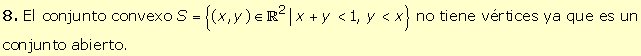 |
|
9.
La
función f(x,y)= 2x +3y es lineal por
tanto, es cóncava y convexa en
R2. |
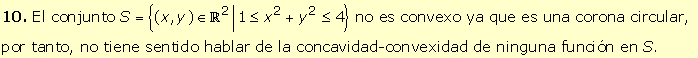 |
|
 |
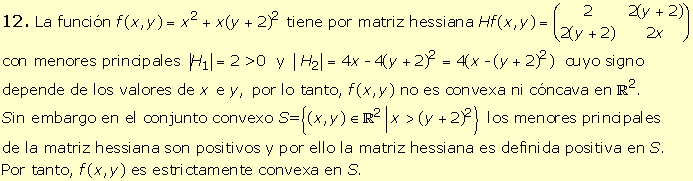 |
 |
 |
 |
Volver a página inicial
|